多层神经元网络
　　一个网络可以有几层，每一层都有权重矩阵W，偏置向量b和输出向量a。为了区分这些权重矩阵、输出矩阵等等，在图中的每一层，我们都为感兴趣的变量以上标的形式增加了层数。你能够看到在下面所示的三层网络图和等式中使用层符号。

　　
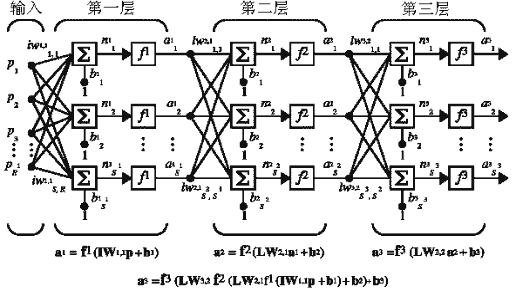
　　上面所示的网络有R1个输入，第一层有S1个神经元，第二层有S2个神经元，以次类推。一般不同层有不同数量的神经元。每一个神经元的偏置输入是常量1。
　　注意中间层的输出就是下一层的输入。第二层可看作有S1个输入，S2个神经元和S1xS2 阶权重矩阵W2 的单层网络。第二层的输入是a1，输出是a2，现在我们已经确定了第二层的所有向量和矩阵，我们就能把它看成一个单层网络了。其他层也可以照此步骤处理。
　　多层网络中的层扮演着不同的角色。给出网络输出的层叫做输出层。所有其他的层叫做隐层。上图所示的三层网络有一个输出层（第三层）和两个隐层（第一和第二层）。有些作者把输入作为第四层，这里不用这种指定。
　　上面所示的三层网络的简洁画法如下图所示：

　　
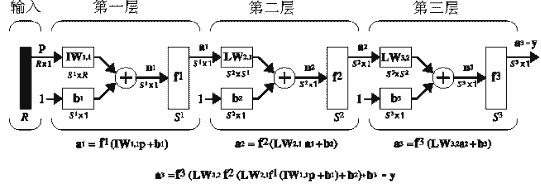
　　多层网络的功能非常强大。举个例子，一个两层的网络，第一层的转移函数是曲线函数，第二层的转移函数是线性函数，通过训练，它能够很好的模拟任何有有限断点的函数。这种两层网络集中应用于"反向传播网络"。
注意我们把第三层的输出a3标记为y。我们将使用这种符号来定义这种网络的输出。

　　4．数据结构
　　这一节将讨论影响网络仿真的输入数据结构的格式。我们首先讨论静态网络，在讨论动态网络。
　　我们将关心两种基本的输入向量类型：同步（同时或者无时序）向量和异步向量。对异步向量来说，向量的顺序是非常重要的。对同步向量来说，顺序是不重要的，并且如果我们已经有一定数量的并行网络我们就能把一个输入向量输入到其中的任意网络。
　　静态网络中的同步输入仿真
　　仿真静态网络（没有反馈或者延迟）是网络仿真最简单的一种。在这种情况中，我们不需要关心向量输入的时间顺序，所以我们可以认为它是同时发生的。另外，为了是问题更简单，我们假定开始网络仅有一个输入向量。我们用下面的网络作为例子。
　　为了建立这个网络我们可以用以下命令：

　　
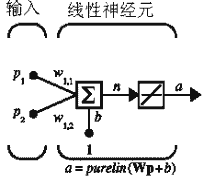
　　net = newlin([-1 1;-1 1],1);
　　简单起见我们假定权重矩阵和偏置为：
　　W=[1，2]，b=[0]
　　其命令行是：
　　　net.IW{1,1} = [1 2];
　　　net.b{1} = 0;
　　假定模拟的网络有四个无序向量，即Q=4：
　　
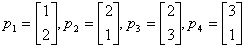
　　这些同步向量可以用一个矩阵来表示：
　　P = [1 2 2 3; 2 1 3 1];
　　现在我们就可以模拟这个网络了：
　　A = sim(net,P)
　　A =
　　5 4 8 5
　　我们向网络输入一个简单的同步向量矩阵，得到了一个简单的同步向量输出矩阵。结果不论是由一个网络串行输出还是由四个网络并行输出得到的都是一样的。由于输入并无关联，输入向量的顺序并不重要。
　　动态网络中的异步输入仿真
　　当网络中存在延迟时，顺序发生的输入向量就要按一定的序列输入网络。为了演示这种情况，我们用了一个有延迟的简单网络。
　　
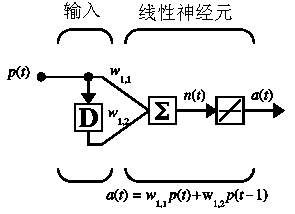
　　为了建立这个网络我们可以用以下命令：
　　net = newlin([-1 1],1,[0 1]);
　　net.biasConnect = 0;
　　假定权重矩阵为：
　　W=[1，2]
　　命令行为：
　　net.IW{1,1} = [1 2];
　　假定输入顺序为：
　　p(1)=[1], p(2)=[2],p(3)=[3], p(4)=[4]
　　输入序列可以用一个细胞数组来表示：
　　P = {1 2 3 4};
　　这样我们就能模拟这个网络了：
　　A = sim(net,P)
　　A =
　　[1] [4] [7] [10]
　　我们输入一个包含输入序列的细胞数组，网络产生一个包含输出序列的细胞数组。注意异步输入中的输入顺序是很重要的。在这个例子中，当前输出等于当前输入乘1加上前一个输入乘2。如果我们改变输入顺序，那么输出结果也回随之改变。
　　动态网络中的同步输入仿真
　　如果我们在上一个例子中把输入作为同步而不是异步应用，我们就会得到完全不同的响应。（虽然我们不清楚为什么要在动态网络中使用这种方式。）这就好象每一个输入都同时加到一个单独的并行网络中。在前一个例子中，如果我们用一组同步输入，我们有：
　　p1=[1], p2=[2],p3=[3], p4=[4]
　　这可用下列代码创建：
　　P =[1 2 3 4];
　　模拟这个网络，我们得到：
　　A = sim(net,P)
　　A =
　　1 2 3 4
　　这个结果和我们同时把每一个输入应用到单独的网络中并计算单独的输出没什么两样。注意如果我们没有初始化延迟时间，那么缺省值就是0。在这个例子中，由于当前输入的权重是1，输出就是输入乘1。在某些特定的情况下，我们可能想要在同一时间模拟一些不同序列的网络响应。这种情况我们就要给网络输入一组同步序列。比如说，我们要把下面两个序列输入网络：
　　p(1)=[1], p(2)=[2],p(3)=[3], p(4)=[4]
　　p(1)=[4], p(2)=[3],p(3)=[2], p(4)=[1]
　　输入P应该是一个细胞数组，每一个数组元素都包含了两个同时发生的序列的元素。
　　P = {[1 4] [2 3] [3 2] [4 1]};
　　现在我们就可以模拟这个网络了：
　　A = sim(net,P);
　　网络输出结果将是：
　　A = {[ 1 4] [4 11] [7 8] [10 5]}
　　你可以看到，每个矩阵的第一列是由第一组输入序列产生的输出序列，每个矩阵的第二列是由第二组输入序列产生的输出序列。这两组序列之间没有关联，好象他们是同时应用在单个的并行网络上的。
　　下面的图表显示了当我们有Q个TS长度的序列时，在函数sim中输入P的一般格式。它函盖了单输入向量的所有的情况。每一个细胞数组的元素都是一个同步向量矩阵，它对应于每一个序列的同一时间点。如果有多输入向量，那么在细胞数组中的矩阵里就有多行。

　　
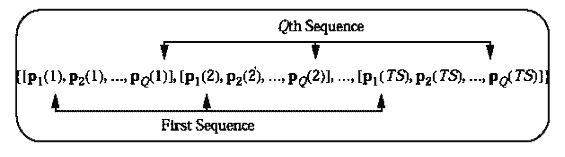
　　这一节我们我们把同步和异步输入应用到了动态网络中。在以前的章节中我们把同步输入应用到了静态网络中。我们也能把异步序列应用到静态网络中。这不会改变网络的输出响应，但是这会影响训练过的网络的形式。在下一节你会更清楚的了解这一点。

　　5．训练方式
　　在这一节中，我们将描述两种不同的训练方式。在增加方式中，每提交一次输入数据，网络权重和偏置都更新一次。在批处理方式中，仅仅当所有的输入数据都被提交以后，网络权重和偏置才被更新。
　　增加方式（应用与自适应网络和其他网络）
　　虽然增加方式更普遍的应用于动态网络，比如自适应滤波，但是在静态和动态网络中都可以应用它。
在这一节中我们将示范怎样把增加方式应用到这两种网络中去。
　　静态网络中的增加方式
　　继续考虑前面用过的第一个静态网络的例子，我们用增加方式来训练它，这样每提交一次输入数据，网络权重和偏置都更新一次。在这个例子里我们用函数adapt，并给出输入和目标序列：
　　假定我们要训练网络建立以下线性函数：
　　t=2p1+p2
　　我们以前用的输入是：
　　
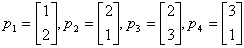
　　目标输出是：
　　t1=[4],t2=[5] ,t3=[7] ,t4=[7]
　　我们首先用0初始化权重和偏置。为了显示增加方式的效果，我们把学习速度也设为0。
　　net = newlin([-1 1;-1 1],1,0,0);
　　net.IW{1,1} = [0 0];
　　net.b{1} = 0;
　　为了用增加方式，我们把输入和目标输出表示为以下序列：
　　P = {[1;2] [2;1] [2;3] [3;1]};
　　T = {4 5 7 7};
　　前面的讨论中，不论是作为一个同步向量矩阵输入还是作为一个异步向量细胞数组输入，模拟的输出值是一样的。而在训练网络时，这是不对的。当我们使用adapt函数时，如果输入是异步向量细胞数组，那么权重将在每一组输入提交的时候更新（就是增加方式），我们将在下一节看到，如果输入是同步向量矩阵，那么权重将只在所有输入提交的时候更新（就是批处理方式）。
　　我们现在开始用增加方式训练网络：
　　[net,a,e,pf] = adapt(net,P,T);
　　由于学习速度为0，网络输出仍然为0，并且权重没有被更新。错误和目标输出相等。
　　a = [0] [0] [0] [0]
　　e = [4] [5] [7] [7]
　　如果我们设置学习速度为0.1，我们就能够看到当每一组输入提交时，网络是怎么调整的了。
　　net.inputWeights{1,1}.learnParam.lr=0.1;
　　net.biases{1,1}.learnParam.lr=0.1;
　　[net,a,e,pf] = adapt(net,P,T);
　　a = [0] [2] [6.0] [5.8]
　　e = [4] [3] [1.0] [1.2]
　　由于在第一个输入数据提交前还没有更新，第一个输出和学习速率为0时一样。由于权重已更新，第二个输出就不一样了。每计算一次错误，权重都不断的修改。如果网络可行并且学习速率设置得当，错误将不断的趋向于0。
　　动态网络中的增加方式
　　我们同样也能用增加方式训练动态网络。实际上，这是最普遍的情况。让我们用前面用过的那个有输入延迟的线性网络作为例子，我们将初始化权重为0，并把学习速率设为0.1。
　　net = newlin([-1 1],1,[0 1],0.1);
　　net.IW{1,1} = [0 0];
　　net.biasConnect = 0;
　　为了用增加方式，我们把输入和目标输出表示为细胞数组的元素：
　　Pi = {1};
　　P = {2 3 4};
　　T = {3 5 7};
　　这里我们尝试训练网络把当前输入和前一次输入加起来作为当前输出。输入序列和我们以前使用sim的例子中用过的一样，除了我们指定了输入序列的第一组作为延迟的初始状态。现在我们可以用adapt来训练网络了：
　　[net,a,e,pf] = adapt(net,P,T,Pi);
　　a = [0] [2.4] [ 7.98]
　　e = [3] [2.6] [-1.98]
　　由于权重没有更新，第一个输出是0。每一个序列步进，权重都改变一次。
　　批处理方式
　　在批处理方式中，仅仅当所有的输入数据都被提交以后，网络权重和偏置才被更新，它也可以应用于静态和动态网络。我们将在这一节讨论这两种类型。